HALO MEASUREMENTS:
INDEX OF REFRACTION
Clifford E Carnicom
September 1 2000
Edited May 24 2013
Edited May 29 2013
(See Below)
Halo Measurements – Index of Refraction
A method has been developed to determine the index of refraction of the materials in the sky that produce the halos that are now commonly observed as a direct result of aircraft activity in our skies. Correspondingly, the angle of the halo can also be determined from this method. The significance of this method is that the chemical and physical nature of ice, as well as historic measurements, establish what the index of refraction and the halo angular measurement are expected to be. If measurements indicate a deviation from that result, it informs us that the materials forming the aircraft-generated halos, cirrus and cirro-stratus cloud decks are no longer composed solely of ice as is often claimed.
The measurements do indicate such a deviation. Initial halo measurements suggest that the hexagonal prisms of uniform size and associated cirrus and cirro-stratus cloud decks are not composed solely of ice as is usually claimed. These measurements and results are preliminary, and will be either refuted or confirmed by further observations in the future.
The method is as follows:
The index of refraction can be determined by:
n = sin ½ (A+D) / sin ½ A
where
n = index of refraction
D = minimum angle of deviation of a prism
A = refracting angle of a prism
In the case of ice, n = 1.310 in the middle of the visible light spectrum. In the case of water, n = 1.330. In the case of a hexagonal prism, which most often is the type of prism that forms the now commonly observed halos, A = 60 degrees. (360deg. / 6)
The angle D can then be solved for as:
D = 2 [arcsin(nsin1/2A)]-A
or D = 21deg. 50min. 30”sec.
This value agrees extraordinarily well with observed historic measurements of the halo phenomenon. In fact, halo measurements are sometimes used as a form of calibration for angular measurements. Two reliable sources confirm this expected value:
1. Vincent Schaefer, inventor of cloud seeding in 1946, states the expected measurement as 21deg. 51min.
2. M. Minnaert, The Nature of Light and Colour in the Open Air, states the best measurements as being 21deg. 50min.
These two sources, as well as their combined average, agree with all expected results of both physics and chemistry.
A method to measure the halo angle videogrammetrically has been established. This method is as follows:
1. The equivalent focal length of the video camera used has been determined by field calibration at 167mm producing a captured image size of 105mm(10.5cm) along the horizontal (long) axis. The expected error (sample standard deviation) of this focal length determination is +/- 3mm.
2. The angle of view of the captured image along the long axis is therefore: Angle of view = 2arctan(5.25cm/16.70cm) = 34.9033deg.
3. Captured images were doubled to size at 21.00cm along the x axis. Measurements were taken from 3 separate captured images from the inside of the visible ring to the center of the sun. Images were taken in a negative view to filter sunlight and provide a more definite point of measurement. Measurements were 127mm, 128mm, and 129mm respectively. The average of these measurements is 128mm and the sample standard deviation is 0.8mm.
4. The angular view of the observed halo is therefore (12.80cm/21.00cmm) 34.9033deg = 21deg. 16min. which deviates from the expected value of 21deg. 50min. This is the first indication by this method that suggests the refractive material of the prisms that produce the halos is not commensurate with the expected value associated with ice. The index of refraction associated with this
angular measurement is 1.302.
5. It is now equally important to evaluate the expected error of the method which has been developed.
6. The angle of view of the halo, from the videogrammetric method developed is: D = (d / 21cm) * 2arctan(5.25/f) where d = the measured axis from the center of the sun to the inside ring of the halo as imaged on the captured video still. f = the equivalent calibrated focal length of the camera in cm.
7. Applying the law of propagation of variances, the
expected error in A is:
deltaD = sqr[((2arctan(5.25cm/f))/21cm)^2 * deltad^2 + ((2(5.25)d)/21f(1+(5.25^2/f^2)))^2 * deltaf^2]
where
deltaD = the expected error in the angle of the halo as determined by this method.
deltad = the expected error in the image measurement
(.08cm)
deltaf = the expected error in the equivalent calibrated
focal length (3mm)
This leads to an expected error in the angle of the measured halo at 0deg 10min.
8. A statistical test can then be applied to these results to determine if the measured halo departs significantly from the results expected by “normal” atmospheric
chemistry and physics.
9. The t statistic can be computed as:
t = (sqr(n) ( 21deg.50min – 21deg 16min) ) / .167deg
or
t = 3.39
With a sample size of 3 measurements, the results are statistically significant at the 90% level.
The methods developed and described within this article indicate that current atmospheric conditions, with regard to atmospheric halos and their relation to the index of refraction of the physical materials in the skies, are potentially statistically significantly different than the expected norms as determined both by historical measurement and from the expected results of both chemical and physical properties of the atmosphere. This study provides a further basis for direct analysis and sampling of the aerosol particles that are repeatedly observed and directly associated with unidentified aircraft operations across the country since early 1999. These results add to the basis for investigation established earlier by relative humidity studies in the Santa Fe, NM region.
Any errors in this study will be corrected if and as they are discovered.
Clifford E Carnicom
September 1 2000
Edit May 29 2013:
I have revisited the computations and method of this paper in a more thorough sense with consideration of the comments below. My conclusions from that review are as follows:
1. The method outlined above remains as a viable approach to the remote determination of significant deviations in the index of refraction of ice crystal halo formations.
2. One physical error and one numerical error existed in my original computations ; I also find two differences (one physical, one in error analysis approach) in the numerical values within the method outlined below by the reviewer. The net effect of all errors and approaches considered is a statistical wash, and no direct conclusions can be drawn in either case. I am in complete agreement that the index of refraction for the red portion of the spectrum is more appropriate to use vs. the middle of the visible spectrum and I record this as an error of generality on my part using textbook models. My numerical error was a lack of radian to degree conversion during one portion of the error analysis for the problem. My contest with the reviewer approach below will include a non-referenced specific wavelength-index of refraction combination and a lack of use of the law of propagation of variances (squared terms) in the error analysis.
3. The simple remedy to the above situation is to simply collect more data and measurements, as is mentioned within the edit of May 24 2013 by CEC. Continuation of discussion on this limited data set will be equivalently limited at this point. Acquisition of additional data is available to all parties and, if circumstances permit, I may repeat the methods here in the future.
My revisions to this paper would now include the following adjustments:
I will use an index of refraction for the red portion of the spectrum as 1.306 *vs. 1.3072 per the reviewer. My source for this is : The 22o Halo from the Physics and Astronomy Division of Georgia State University. This wll lead to a theoretical value of the halo angle as 21 deg 32.2 min. vs. the photogrametrically measured value of 21 deg 16 min. leading to a deviation of 16 min (vs. an original deviation computed as 34 min. Numerous sources, including the one above, list a suitable value for the red portion of the visible spectrum of 660 nm (+/- 4nm).
The corrected error analysis from my side leads to a standard error of 24 min (my previous value was 10 min of arc) of arc vs the differential approach of 29.5 min from the reviewer below. The z-score associated with my value will be .666 leading to a probability significance of 49%. This value is statistically degraded compared to the original result and it leads to the statistical wash mentioned above.
Additional work on this particular data set will be of insufficient academic and physical interest. My appreciation is extended to the review of the article and with the advances in camera technology, I hope that others will collect additional data and pursue the method. The original deviation as determined remains of interest and of potential significance; additional data trials will be required to determine any statistical conclusions.
Sincerly,
Clifford E Carnicom
May 29 2013
Edit May 24 2013:
The following comments have been received on May 20, 2013 and they are presented to the public through this site as an adjunct to the original paper. My time for reviewing this paper from 2001 is limited, and my response will be brief at this time and will follow the submission presented below: CEC
* * * * *
“Dear Mr Carnicom,
The equations are correct, but the result is valid only for the middle of the visible spectrum. Later the distance at the photos between the center of the sun and inner part of halo ring is measured. This means that n refraction index should be changed to 1.3072 (the middle of red part of the visible spectrum). The D angle now becomes 21 deg. 37 min. 37.77 sec.
Partial derivatives (D in degrees):
a) for d: f(d) = d/21*2*arctg(5.25/16.7) = 1.662061807*d. The partial derivative is 1.662061807 and the part of absolute error 1.662061807*0.08 = 0.1329649446 (degrees).
b) for f: f(f) = 12.8/21*2*arctg(5.25/f) = 1.219047619*arctg(5.25/f). The partial derivative in radians is -20479954636/(3199992912*f^2+88199804637) (computed with http://www.numberempire.com/). Substituting f = 16.7 gives us -0.0208842 (the absolute value is 0.0208842) and the absolute error = 0.0208842*0.3 = 6.26526e-3. In degrees this is 0.3589729556.
Total error is 0.1329649446+0.3589729556 = 0.4919379 (degrees) = 0 deg. 29 min. 30.98 sec.
The real value of D is 21 deg. 16 min. +- 0 deg. 29 min. 30.98 sec. The precomputed value of 21 deg. 37 min. 37.77 sec is within the error margin.
[Name withheld pending permission – CEC]
I may visit this paper again as time permits. In the interim, however, my brief response is as follows:
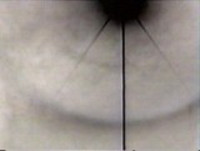
It seems to me that the conclusions presented immediately above are entirely sensible and correct, and that the primary conclusion of the original paper is indeed false. It is of interest that the original image that the work was based on apparently is not within this original document. I have found one image that may have been the inspiration for the project to begin with:
This particular image is of such low resolution is that it only can serve as a reference thumbnail for the project design. Looking back at this image, paper, and memories from more than a decade ago, it strikes me that the measurement was taken from the inside of the ring since that is where a sharp delineation in the ring begins. This, from the analysis above, may simply be inadequate and mispresentative of the spectrum. I will assume that this is the case at this point. The primary value of this paper, therefore, would seem to be the offering of a potential method to remotely investigate the composition of crystalline halos in the atmosphere. This value may still exist, but the topic will need to be revisited. My suggestion at this point for those interested in the method and case is to acquire new imagery of much higher resolution, as it should be readily available to us with improved cameras. The methods can then be reapplied to determine if it is viable or not. Error analysis will remain as a significant consideration, as it is expressed in the original paper as well as by the current reviewer. It is quite possible that even if such atmospheric differences exist that the angular difference detections could be on the order of seconds as opposed to minutes of arc. Differences of interest may or may not be detectable; the problem will have to be reexamined. Thirty minutes of arc is a relatively gross measurement to begin with, and I am sure that this may be one of the clues that the original measurement simply may be flawed with respect to the reference point. I will keep it as a prospect to acquire new imagery of higher resolution over future months and years, and see if the project might be revisited. Others, as always, are invited to pursue the problem themselves. At the current time I am involved in a rather complex project with significant health implications and my time for research and writing remains highly limited. In the interim, my many thanks to the individual that took the time to visit the paper a decade after its presentation. I can only hope and assume that this process of more extended review of the research will eventually take place; this is as it should be and as it needs to be. Pursuit of truth is independent of any particular researcher; my hope is that more of us will choose to become involved in that path as we understand the implications of the issues before us. Thanks again,
Clifford E Carnicom
May 24 2013